Calculating the cube root of integer perfect cubes

For perfect cubes, it is possible to calculate the root by hand.

For n³, where n is an integer, the method of extracting the root is as follows.

	A	B	Root	Comments
a			n0=n3	Place n3under Root, call this n0
b	1		n1 = n0 - 1	Place 1 under A and subtract from Root, new Root is now n1
c		1		Place 1 under Root_Number_B
d1	2	3		Add 1 to A, add to last B value
e1	4	7	n2 = n1 - 7	Add 2 to A, add to last B value, now subtract new B from Root, new root is now n2
d1	5	12		Add 1 to A, add to last B value
e1	7	19	n3 = n2 - 19	Add 2 to A, add to last B value, now subtract new B from Root, new root is now n3

Repeat the process d and e until root n = 0. The value of the Root_Number e when n = 0 is then added to 2 and the sum is divided by 3 which should give the cube root of n^3.

A real example follows.

4x4x4 = 64, so the cube root of 64 is 4.

A	B	Root
		64
1		63
	1
2	3
4	7	56
5	12
7	19	37
8	27
10	37	0

The value of A when Root = 0 is 10. Adding 2 to 10 and dividing by 3 = 12/3 = 4

Series

The numbers which are subtracted from the Root form a series

S_n = 1 + 7 + 19 + 37 + .....

If one looks at the sum, the number of terms relates to the cube root of the sum itself.

1³ term 1 = 1
2³ term 8 = 1 + 7
3³ term 27 = 1 + 7 + 19
4³ term 64 = 1 + 7 + 19 + 37
.
.
n³ term = 1 + 7 + 19 + 37 + …… + (u_n)

The expression for n³ sum can be in the form

Where

(1st term) 1 = 1
(2nd term) 7 = 1 + 6
(3rd term) 19 = 1 + 6 + 12
(4th term) 37 = 1 + 6 + 12 + 18
.
.

By inspection, we see that each successive term contains 1 + a number of terms values which are multiples of 6. Since the first term is 1, the last term is the 6.(n-1).

(nth term) = 1 + 6 + 12 + 18 + 24 + … … + 6.(n-1)

Inspecting the terms, we find that

• 1 occurs n times
• 6 = 6.1 occurs n-1 times
• 12 = 6.2 occurs n-2 times
• 18 = 6.3 occurs n-3 times
• 24 = 6.4 occurs n-4 times

The term 6.(n-1) will appear n-(n-1) times or just once.

Thus the sum becomes

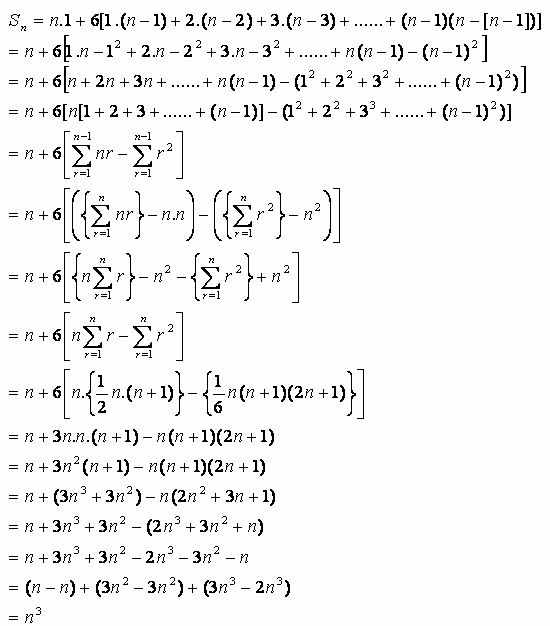
The mathematical summations indicated by the sigma signs are standard identities [Tuckey & Armistead, p.211]. So, from the generalised equation of the summation for

S_n = 1 + 7 + 19 + 37 + ...... + u_n

and identified a

we have found it to be equivalent to the cube of n.

That is,

S_n = n + 6[ (n-1) + 2(n-2) + 3(n-3) + ... + (n-1)(n-[n-1]) ] = n³

Reference

Algebra. C.O. Tuckey & W. Armistead. Longmans, Green and Co., 1958

© Dylan Sung 2005

This page was created on Thursday 2nd June 2005